목차
1. Heap(힙)
2. Height of a Heap(힙의 높이)
3. Heaps and Priority Queues(힙과 우선순위 큐)
1. Heap(힙)
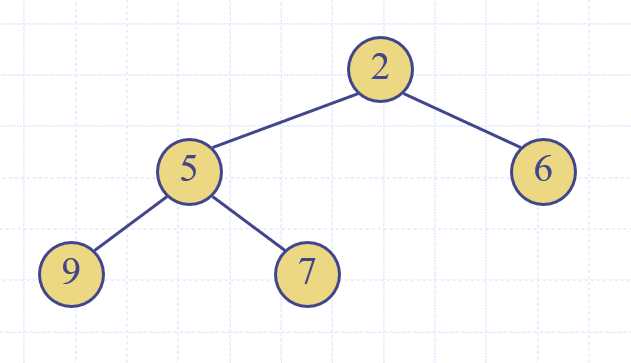
Heap(힙)은 특정한 규칙를 따르고 있는 binary tree입니다. 이 특정한 규칙은,
1) Heap-Order
- 모든 internal node v에 대하여, 자식의 key값이 부모의 key값보다 항상 크거나 같아야 한다.
- (단, root 제외)
- key(v) >= key(parent(v))
2) Complete Binary Tree
- 이전에도 언급하였으나, heap은 complete binary tree를 따라야 한다.
- 이는 모든 레벨의 node가 가득 차있어야 하며, 마지막 레벨의 node는 왼쪽으로 치우쳐있는 binary tree를 의미한다.
- (완전 이진트리이며, v는 왼쪽부터 채워지는 구조)
Heap또한 Priority Queue를 표현하는 하나의 방법으로서, minPQ 혹은 maxPQ를 표현하기 위해 각각 min-heap(최소 힙), max-heap(최대 힙)을 사용합니다.
결론적으로, heap은 1) 일정한 구조를 지닌다, 2) 정해진 순서를 가진다, 이 2가지 개념만 확실하게 생각하면 됩니다.
2. Height of a Heap(힙의 높이)

Heap의 높이는 전체 element의 개수가 n개라고 하였을 때, O(logn)입니다. 그 이유는 heap은 완전 이진트리이며, 왼쪽부터 채워지는 구조이기 때문입니다.
3. Heaps and Priority Queues(힙과 우선순위 큐)

이런 heap을 활용하여 우선순위 큐를 만들 수 있습니다. 각각의 자리에 (key, element)으로 이루어져 있는 item을 넣어서 저장할 것이며, 또한 마지막에 insert, 혹은 remove한 node의 위치를 파악하고 있는 것이 중요합니다.(위치를 알아야 다음 삽입/삭제 시 행동을 취할 수 있기 때문)
'cs > 자료구조' 카테고리의 다른 글
| [Heap]30. Heap-Sort(힙 정렬) (0) | 2021.02.27 |
|---|---|
| [Heap]29. Insertion/Removal from a heap(힙에서의 삽입, 제거) (0) | 2021.02.27 |
| [Priority Queue]27. Priority Queue Sorting(우선순위 큐 정렬) (0) | 2021.02.26 |
| [Priority Queue]26. Priority Queue(우선순위 큐) (0) | 2021.02.26 |
| [Trees]25. Binary Trees Traversal(이진 트리 탐색) (0) | 2021.02.25 |




댓글