목차
1. Insertion into a heap(힙에서의 삽입)
2. Upheap
3. Removal from a heap(힙에서의 제거)
4. Downheap
5. Updating the last node(마지막 node 위치 업데이트)
1. Insertion into a heap(힙에서의 삽입)
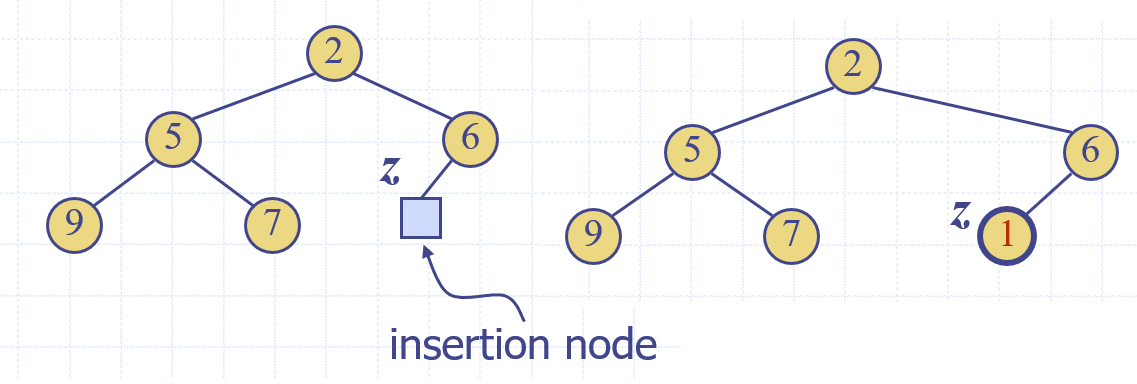
Heap에서 어떤 요소를 삽입하거나 삭제할 경우, heap이 가지는 특성인 1) 구조 맞추기, 2) 순서 맞추기, 이 2가지만 지키면 됩니다. 이중 구조는 일정하기 때문에, 우선 구조를 맞추고, 그 후에 순서를 맞추는 방식을 사용하게 됩니다.
따라서 heap에서 새로운 element를 삽입할 경우,
1) 해당 heap의 마지막 node를 찾고, 새로운 element가 들어갈 node의 위치를 확인한다.
2) 그 자리에 새로 들어온 node를 넣는다.
3) 순서를 바꾼다.
이중 "순서를 바꾼다"를 해결하기 위하여, 아래서 언급하게 될 Upheap을 사용하게 됩니다.
(마지막 insertion node의 위치를 미리 알고있다면, O(1)의 시간 소요)
2. Upheap
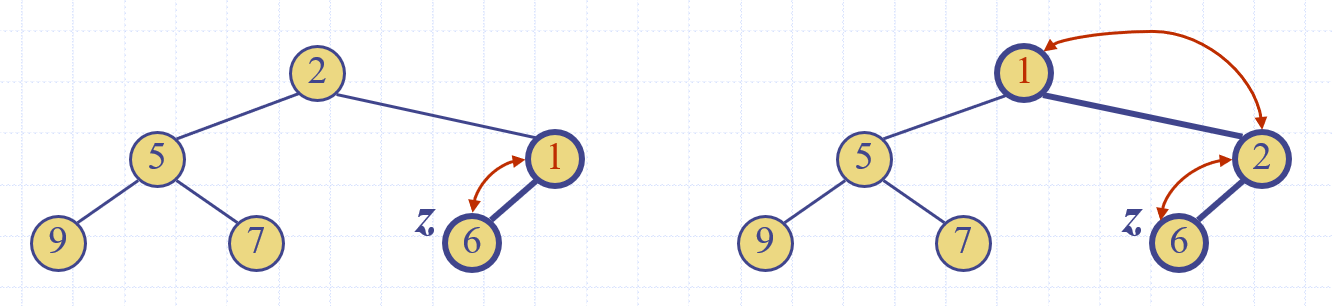
Upheap은 새로운 node가 들어왔을 경우, 이것이 heap의 규칙중 key(v) >= key(parent(v))를 지키기 위한 방법입니다. Upheap이 진행될 경우,
1) 새로 들어온 insertion node와 그의 부모 node를 비교한다.
2) insertion node보다 부모 node가 크다면, 둘의 위치를 교환한다.
3) 1, 2를 heap의 규칙이 성립할 때 까지 계속 반복한다.
따라서 Upheap의 최악의 시간은 O(logn)입니다. (root까지 Upheap이 진행되었을 경우)
3. Removal from a heap(힙에서의 제거)

힙에서의 삽입과 같이, Removal from a heap(힙에서의 제거) 또한 heap의 구조와 순서를 지키면서 제거하면 됩니다. 여기서 생각해볼 점은, min-heap이라고 가정하였을 때 힙에서의 제거는 곧 가장 작은 값 min()을 제거하는 경우입니다. 하지만 heap에서 root을 제거하게 되면, 그 heap은 서로 갈라지게 됩니다.
따라서, Removal from a heap은
1) 마지막 node의 데이터 값을 root의 데이터 값에 덮는다.
2) 마지막 node 지운다.
3) last node 위치 이동한다.
4) 순서를 바꾼다.
이중 "순서를 바꾼다"를 해결하기 위하여, 아래서 언급하게 될 Downheap을 사용하게 됩니다.
(마지막 insertion node의 위치를 미리 알고있다면, O(1)의 시간 소요)
4. Downheap
Downheap은 Upheap과 마찬가지로 새로운 node가 들어왔을 경우, 이것이 heap의 규칙중 key(v) >= key(parent(v))를 지키기 위한 방법입니다. Downheap이 진행될 경우,
1) 새로 들어온 root와 두 자식 중 key의 크기가 작거나 같은 node와 비교한다.
2) root보다 자식 node가 작다면, 둘의 위치를 교환한다.
3) 1, 2를 heap의 규칙이 성립할 때 까지 계속 반복한다.
따라서 Upheap의 최악의 시간은 O(logn)입니다. (external node 까지 Upheap이 진행되었을 경우)
5. Updating the last node(마지막 node 위치 업데이트)
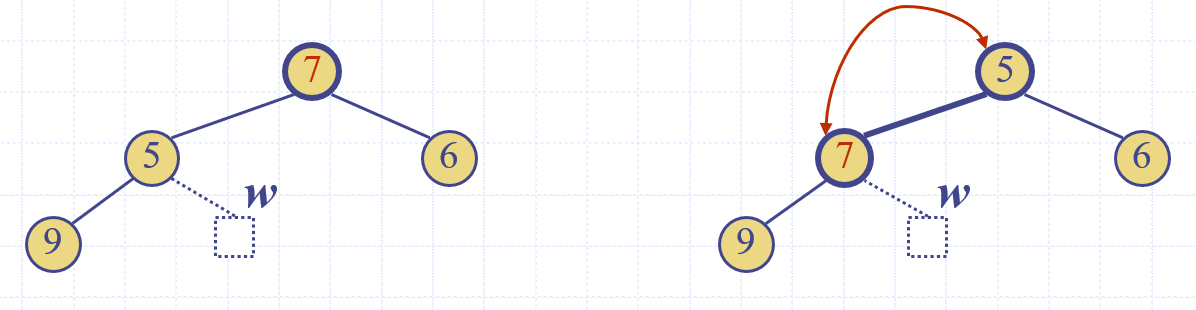
알고리즘적으로 생각해 보았을 때, 새로 입력해야하는 node의 위치는 바로 전에 입력했던 node에서 시작해서 찾을 수 있습니다. 바로 아래의 세가지 규칙을 지켜가면서 node를 이동하면 됩니다.
1) 부모의 왼쪽 자식 혹은 root까지 갈때 까지 올라간다.
2) 만일 부모의 왼쪽 자식에서 멈췄다면, 해당 부모의 오른쪽 자식으로 이동한다.
3) leaf가 나올 때 까지 내려간다.
이렇게 다음 입력될 node를 찾는다면 최악의 경우, O(logn)의 시간이 소요됩니다. 하지만 후 게시물에 언급할 배열(벡터)를 활용하여 heap를 만들 경우, O(1)만에 마지막 node가 들어갈 위치를 찾을 수 있습니다.
'cs > 자료구조' 카테고리의 다른 글
| [Heap]31. Vector(array) Based Heap(벡터(배열)기반 힙) (0) | 2021.02.27 |
|---|---|
| [Heap]30. Heap-Sort(힙 정렬) (0) | 2021.02.27 |
| [Heap]28. Heap(힙) (0) | 2021.02.26 |
| [Priority Queue]27. Priority Queue Sorting(우선순위 큐 정렬) (0) | 2021.02.26 |
| [Priority Queue]26. Priority Queue(우선순위 큐) (0) | 2021.02.26 |




댓글